noip模拟19
目录
2018 雅礼集训 D3
T1
我以后遇到类似的问题再也不会傻不啦叽算重叠面积了
套路:凡是一次修改一大片数据的都可以考虑使用线段树或差分
线段树做法:建两颗树,分别维护斜边和垂直的边的操作(斜边挺复杂)我也没写(逃
一维差分:在每行上差分,列不变。在每行的开始加上S,末尾向后一位减去S。如果出界了就不减了(可以拿47分,TLE的也不多)
正解:二维差分
先来看普通的二维差分: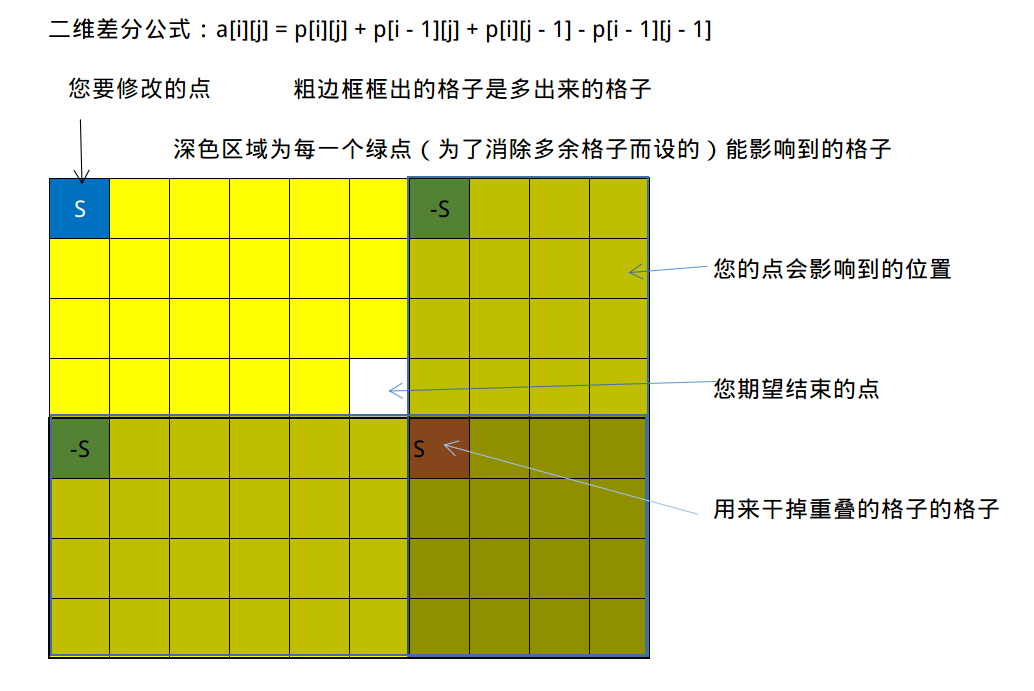
那对于这道题的三角该如何处理呢?
Show you the CODE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>
#define For(i, l, r) for (int i = (l), i##end = (r); i <= i##end; ++i)
#define Fordown(i, r, l) for (int i = (r), i##end = (l); i >= i##end; --i)
#define Set(a, v) memset(a, v, sizeof(a))
using namespace std;
const int maxn = 3010;
template <class type>
type read() {
type s = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
s = s * 10 + ch - '0';
ch = getchar();
}
return s * f;
}
struct POINT {
int x, y, l, s;
} pnt[300005];
long long lower[maxn][maxn], sum[maxn][maxn];
int main() {
int n, m;
n = read<int>(), m = read<int>();
for (int i = 1; i <= m; i++) {
pnt[i].x = read<int>(), pnt[i].y = read<int>(), pnt[i].l = read<int>(),
pnt[i].s = read<int>();
if (pnt[i].x <= n && pnt[i].y <= n) {
sum[pnt[i].x][pnt[i].y] += pnt[i].s;
}
if (pnt[i].x + pnt[i].l <= n && pnt[i].y + pnt[i].l <= n) {
sum[pnt[i].x + pnt[i].l][pnt[i].y + pnt[i].l] -= pnt[i].s;
}
if (pnt[i].x + pnt[i].l <= n && pnt[i].y <= n) {
lower[pnt[i].x + pnt[i].l][pnt[i].y] -= pnt[i].s;
}
if (pnt[i].x + pnt[i].l <= n && pnt[i].y + pnt[i].l <= n) {
lower[pnt[i].x + pnt[i].l][pnt[i].y + pnt[i].l] += pnt[i].s;
}
}
long long ans = 0;
For(i, 1, n) {
For(j, 1, n) {
if (i >= 2) {
sum[i][j] += sum[i - 1][j] + sum[i - 1][j - 1] - sum[i - 2][j - 1];
} else {
sum[i][j] += sum[i - 1][j] + sum[i - 1][j - 1];
}
lower[i][j] += lower[i - 1][j] + lower[i][j - 1] - lower[i - 1][j - 1];
ans ^= (sum[i][j] + lower[i][j]);
}
}
printf("%lld\n", ans);
return 0;
}